Statistische Grundbegriffe

Statistik als ein Grundpfeiler von Wissenschaftlichkeit

Korrelation und Regression

Ergibt eine Studie eine Korrelation zwischen zwei Variablen, bedeutet dies einen möglichen Zusammenhang zwischen den zwei Größen (z.B. Variable A steigt zweimal so schnell wie Variable B; A = 2⋅B). Zu bedenken ist, dass sich eine Korrelation rein zufällig ergeben kann. Die Anzahl "falscher" Korrelationen steigt dabei mit der Anzahl der untersuchten Variablen.
Aus einer Korrelation kann mittels Regression eine Funktion abgeleitet werden, die kausale Zusammenhänge zwischen Variablen beschreibt. Die Aussagekraft der Regression hängt von der Qualität der Interpretation, der ihr zugrundeliegenden Korrelaton ab.

Erwartungswert, Streuung und Normalverteilung

Der Erwartungswert μ beschreibt die Summe aller möglichen Ergebnisse einer Zufallsfunktion, multipliziert mit ihrer theoretischen Wahrscheinlichkeit. Im Falle eines Wüfelwurfs ergibt sich für den Erwartungswert: (1+2+3+4+5+6)⋅⅙ = 3,5 (je öfter der Würfelwurf durchgeführt wird, desto mehr nähert sich der Mittelwert dem Erwartungswert)
Für die Streuung einer Zufallsverteilung (Abweichung vom Erwartungswert) wird auf die Größen Standardabweichung σ und Varianz σ² zurückgegriffen.
In einer Normalverteilung bestimmt der Erwartungswert μ die Position ihres Maximums und "verschiebt" die Kurve nach links oder rechts. Die Varianz σ² sorgt für die Streuung der Ergebnisse: bei höherer Varianz verläuft die Kurve flacher und bei niedrigerer Varianz spitzer.

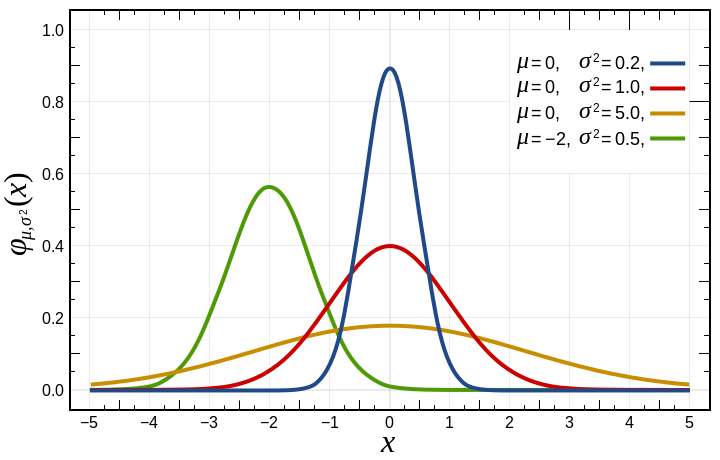Normalverteilungen finden in den unterschiedlichsten Bereichen Anwendung: bei Finanzanalysen, medizinischen und sozialwissenschaftlichen Studien oder im Produktionsmanagement. Dabei können nicht alle Bereiche gleich behandelt werden, sondern müssen abhängig von ihrem Verhalten differenziert werden. Statistische Verteilungen, die eine geringe Streuung aufweisen, können ziemlich gut mit einer Normalverteilung beschrieben werden. Die Ausreißer nach oben, wie nach unten, haben geringe Auswirkungen auf die Funktion. "Wildere" Verteilungsfunktionen, können hingegen viel besser mit fraktalen Verteilungen beschrieben werden. Der Einsatz von Normalverteilungen im Risikomanagement der Finanzbranche, ist mit ein Grund für das Versagen der Finanzmärkte. Entscheidend ist nicht die Häufigkeit des Auftretens einer Abweichung, sondern ihre langfristige Auswirkung auf das Gesamtsystem. Fraktale Analysen bieten hier eine Möglichkeit unwahrscheinliche, aber verheerende Werte einzubeziehen und Risiken besser zu erkennen.

Stichproben, Signifikanz und Effektstärke

Bei statistischen Untersuchungen wird aus eine Grundgesamtheit (z.B. alle Männer in Deutschland über 40) eine Stichprobe entnommen. Auf Basis des Gesetzes der großen Zahlen ergibt sich der minimal erforderliche Stichprobenumfang, der die Repräsentativität der Studie sicherstellt. Zu bedenken ist, dass die gemessene statistische Signifikanz nicht gleich der praktischen Relevanz einer Studie ist. Die praktische Signifikanz einer Studie wird vielmehr von ihrer (relativen) Effektstärke ausgedrückt, da diese im Gegegnsatz zur statistischen Signifikanz, unabhängig von der Stichprobengröße ist (geringere Manipulationsmöglichkeiten durch Stichprobenauswahl). Die Betrachtung absolute Effektstärke (Mittelwert1 - Mittelwert2) ermöglicht die bessere Vergleichbarkeit von Studien, durch die Unabhängigkeit von Varianzen.

Klassifizierung

Eine Klassifizierung von Variablen und Daten ist für wissenschaftliche Konzepte oder das Data Mining von Bedeutung. Klassifikation kann mittels Faktorenanalysen oder Clusteranalysen vorgenommen werden. Die Klassifizierbarkeit von Variablen hängt, neben dem Klassifikationsverfahren, von der Stichprobengröße und Datenstruktur ab.

Verantwortlich: Ioannis Alexiadis

Prognosen Risikokompetenz Medizinische Studien Messwerte